티스토리 뷰
[무료] 혼자 공부하는 머신러닝+딥러닝 - 인프런 | 강의
한빛미디어 혼공시리즈로 1:1 과외하듯이 배우는 초절정 머신러닝, 딥러닝 자습서, 수백 개의 손그림으로 이해하고 구글 코랩(Colab)을 통해 브라우저만 있으면 바로 실습 가능, - 강의 소개 | 인프
www.inflearn.com
K-최근접 이웃 회귀

이전 강의에서는 이진 분류를 다뤄보았다. 이진 분류의 target은 항상 0 또는 1의 값을 가진다.
이번 시간에 다룰 회귀(regression)란 둘 중 하나를 예측하는 것이 아니라 임의의 숫자를 예측하는 방법론이다.
=> 회귀의 target: 임의의 숫자

왼쪽의 그림은 이전에 다뤘던 k-최근접 이웃 분류이다. 근접한 클래스의 과반수에 따라 타겟의 클래스를 예측한다.
이번 시간에 다루는 k-최근접 이웃 회귀도 마찬가지로 분류와 동일하다. 근접한 이웃들의 평균을 타겟값으로 정한다.

예제를 단순화하기 위해 농어 길이만으로 농어의 무게를 예측해보도록 하자.
plt.scatter(perch_length, perch_weight)코드에서 perch_length가 주어지는 농어의 길이 값이고, perch_weight이 우리가 예측해야 하는 무게 값(타깃)이다!

from sklearn.model_selection import train_test_split농어 훈련 세트를 준비하기 위해 저번 강의와 동일하게 사이킷런 모듈의 train_test_split 을 사용한다.
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)train_test_split으로 구한 훈련 데이터셋은 train_input, test_input 변수에 1차원 배열로 저장된다.
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)학습 모델에 적용하기 위해서 1차원 배열로 저장된 값들을 2차원 배열로 재구성하도록 한다. (reshape())
예시) [1,2,3] -> [[1],[2],[3]]

편리하게도 사이킷런에는 k-근접이웃회귀 라이브러리가 존재한다. (KNeighborsRegressor)
k-근접이웃분류와 똑같이
knr = KNeighborRegressor()(1) 클래스 객체(knr)를 할당하고
knr.fit(train_input, train_target)(2) fit 메소드로 train_input 데이터와 train_target 데이터를 학습 시킨 다음
knr.score(test_input, test_target)(3) score 메소드로 정확도를 매겨보자.
score 메소드에서 사용되는 회귀 정확도는 R^2 라는 결정 계수이다.
R^2 = 1 - ((타깃 - 예측)^2의 합 / (타깃 - 평균)^2의 합) |
R^2 결정 계수는 0 - 1 사이의 값으로 매겨지며 1에 가까울 수록 정확도가 높음을 의미한다.
결정 계수 외에 다른 지표로도 모델의 성능 판단이 가능하다.
from sklearn.metrics import mean_absolute_errormetrics 모듈의 mean_aboslute_error를 사용하면 예측 값과 실제 값의 차이를 평균 내어 구할 수 있다.
test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)위의 코드에서 test_prediction 변수에는 test_input으로 예측한 결과 값이 들어오는데, mean_absolute_error 메소드를 사용하면 실제 test_target 값과 예측한 test_prediction의 차이값에 대해 절대값 평균을 구한다.
대략 19cm의 오차가 나타난다는 것을 알 수 있다.

연습 문제를 풀었을 때보다 시험 문제를 풀었을 때 성적이 더 잘 나온다면?
( = 학습시킬 때보다 실제로 예측했을 때 더 정확하다면?)
-> 과소 적합 (underfitting)
반대로 학습시킬 때 더 정확하고, 예측했을 때 훨씬 정확도가 떨어진다면?
-> 과대 적합 (overfitting)
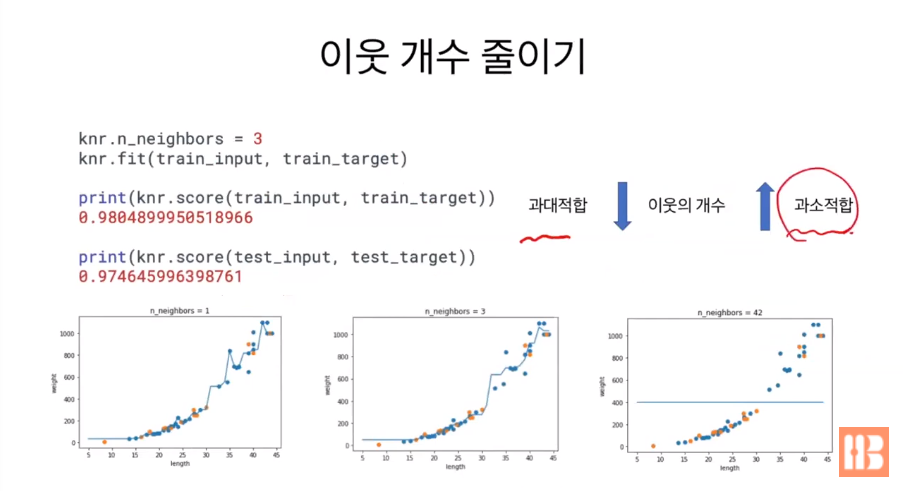
즉, 이웃의 개수가 너무 적으면 과대 적합이 되고 이웃의 개수가 너무 많으면 과소 적합이 된다.
그래서 이전에 사용한 데이터셋에서 이웃 개수를 5 -> 3으로 줄인 다음 재훈련해보았다.
그 결과, 두 값이 동떨어지지 않고 비슷비슷해지면서 적절한 균형점을 찾았다.
선형 회귀
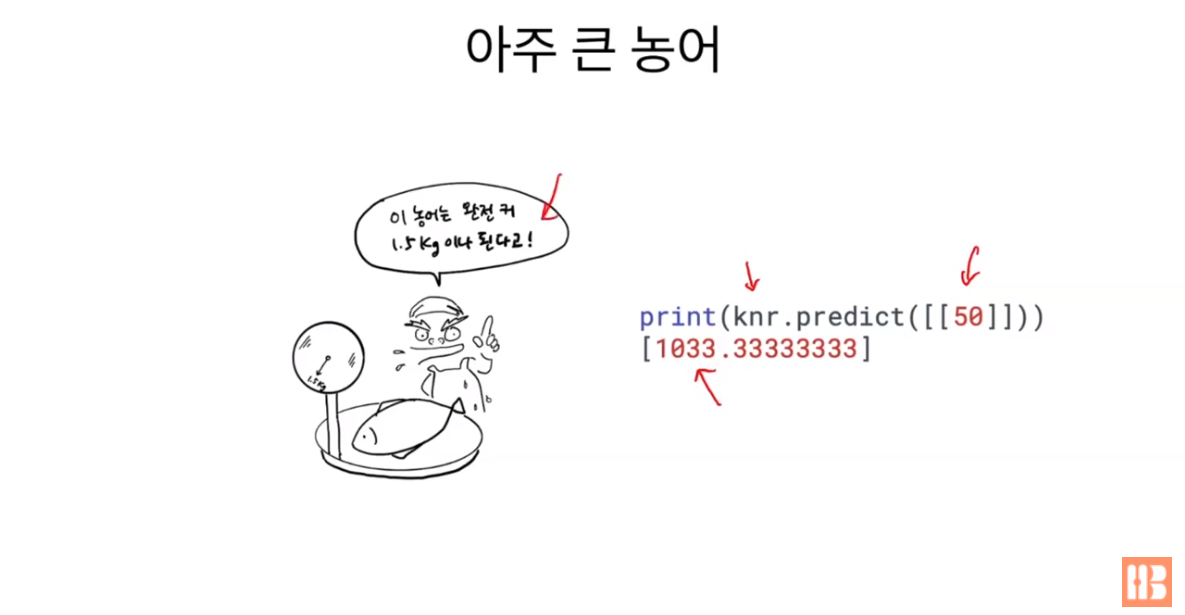
길이가 50cm인 농어의 무게를 우리가 만든 모델로 예측하면 1033kg이 나온다.
하지만 실제 무게는 1.5kg라고 하는데.. 왜 이런 오차가 발생하는 걸까?
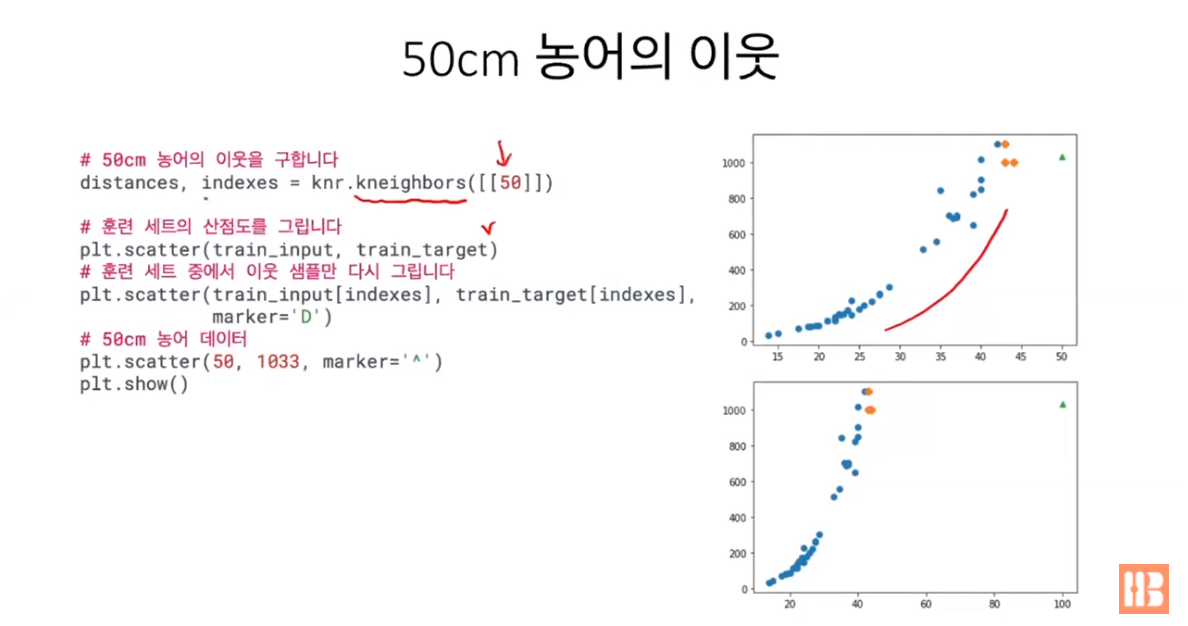
산점도를 그려서 이유를 살펴보자.
삼각형이 우리의 타겟 값이고, 주황색 다이아몬드가 K개의 이웃이다.
K-이웃 회귀는 이웃 내부에 있는 값은 정확하게 예측하지만, 그래프 외부에 있는 데이터는 잘 예측하지 못한다고 한다.
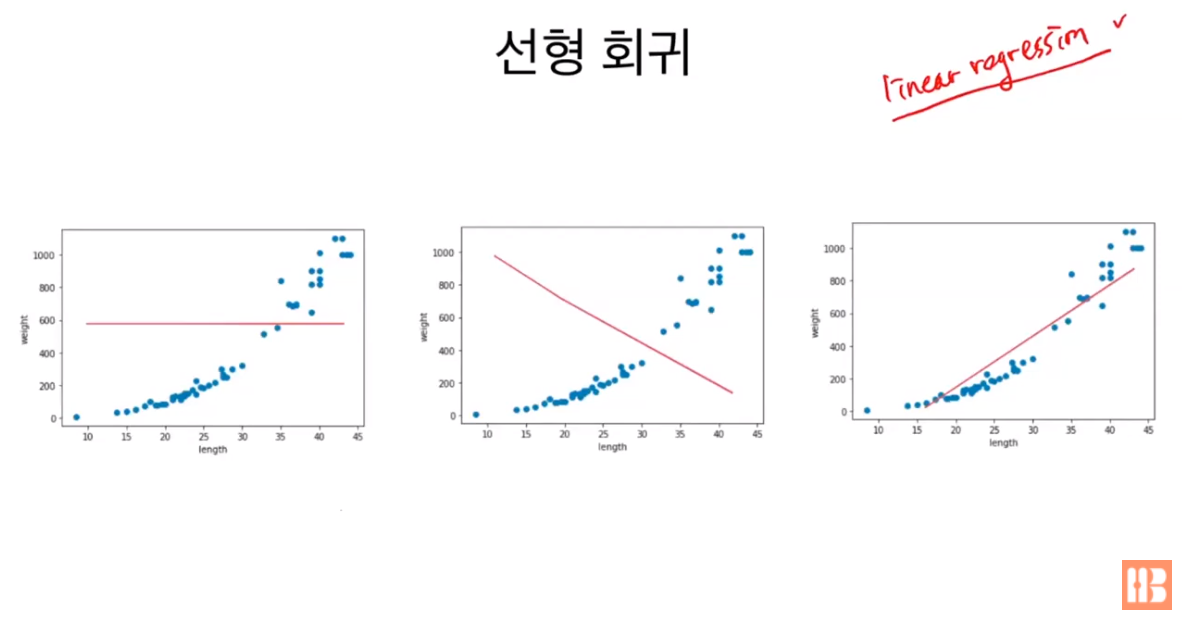
이 문제를 해결할 수 있는 방법은 '선형 회귀'(Linear Regression)이다. 선형 회귀란 그래프를 가장 잘 나타내는 직선을 찾는 방법론으로 위의 그림에서는 3번째 직선이 이에 해당한다.

싸이킷런에는 선형 회귀 라이브러리가 존재한다. (linear_model 모듈) 클래스 객체를 생성하고 fit으로 모델을 훈련시킨 다음, predict 메소드로 50cm 농어의 무게를 예측한다. 이 때, 직선 방정식으로 농어의 무게를 나타낼 수 있기 때문에 `농어 무게(y) = a(기울기) * 농어 길이(x) + b(y절편)` 이라는 공식이 성립한다. 여기서 a는 coef_로, 그리고 b는 intercept_로 클래스 객체에서 불러올 수 있다.
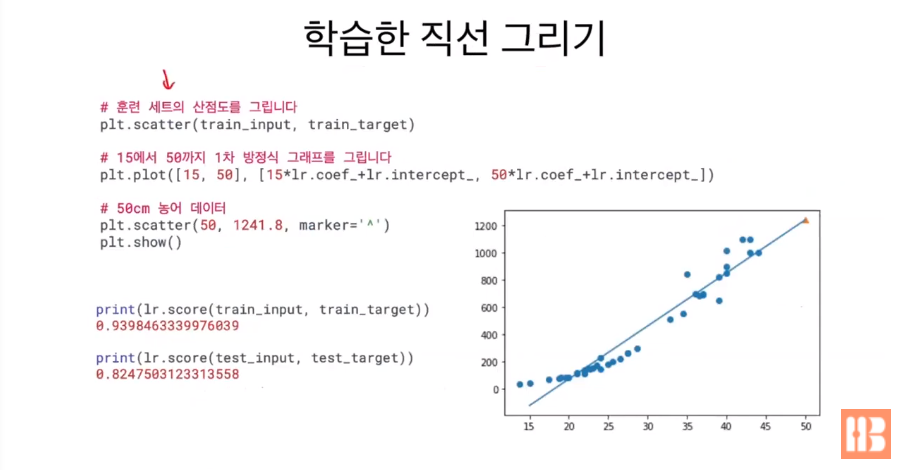
학습한 직선을 산점도로 그려보자.
score로 정확도를 매기면 학습 데이터의 정확도에 비해 테스트 값 정확도가 너무 낮다는 것을 확인할 수 있다.
=> 과대적합
또 하나의 문제는 직선 방정식 시작 부분에서 농어의 무게가 음수로 떨어지는 것을 확인할 수 있다. 길이가 짧으면 무게가 마이너스가 되어버리는 오류가 발생하기 때문에 1차 방정식을 2차 방정식으로 바꿔 문제를 해결해야 한다.
(점들의 위치만 봐도 직선보다는 곡선이 더 잘 맞을 것 같음 .. )
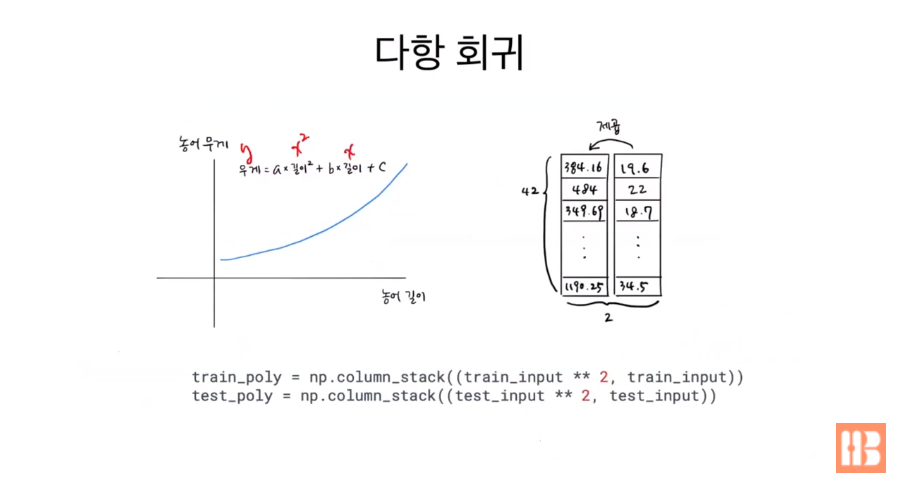
2차 방정식 꼴로 곡선의 그래프를 구하는 방법을 다항 회귀라고 한다. 직선 방정식과 달리 길이^2(x^2)의 값이 필요하기 때문에 열을 하나 추가해 길이^2의 값을 저장한 배열을 만든다.

1차 방정식과 똑같은 순서로 모델을 다시 훈련한다.
=> y = 1.01x^2 - 21.6x + 116.05
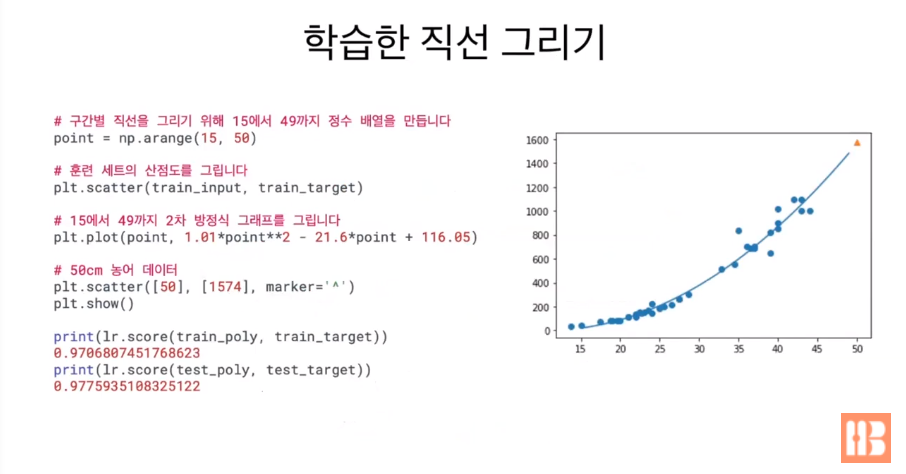
point = np.arange(15, 50)길이가 1인 직선을 연속적으로 그려 곡선처럼 표현하기 위해 arange 메소드로 정수 배열을 만든다.
plt.scatter(train_input, train_target)
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)산점도를 그리고, plot 메소드와 아까 만든 정수 배열 point로 2차 방정식 그래프를 그린다.
plt.scatter([50], [1574], marker='^')
plt.show()50cm 농어 데이터를 산점도 위에 그려준다.
score로 정확도를 매기면 두 정확도가 1차 방정식보다 매우 비슷해졌음을 확인할 수 있다.
특성 공학과 규제 알아보기
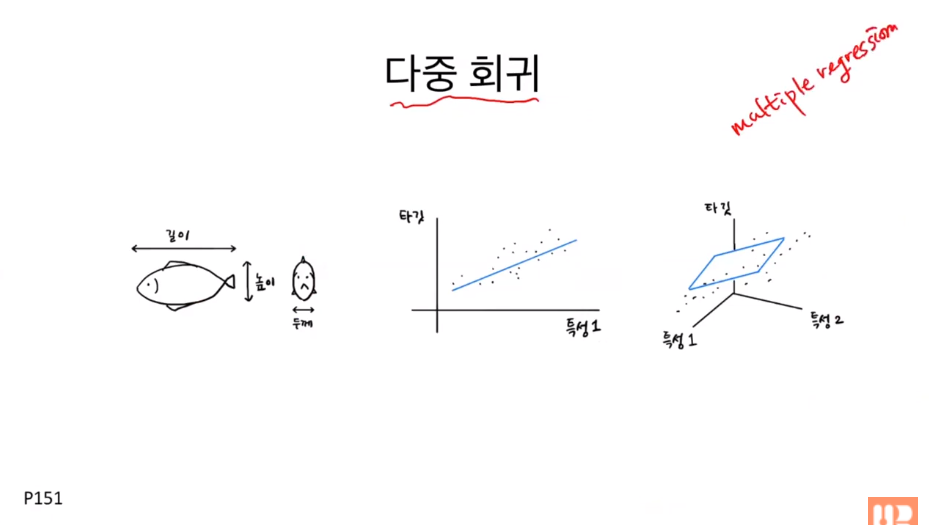
다중 회귀(multiple/multinomial regression)란 여러 개의 변수(특성)를 사용하는 회귀를 말한다. 이번에는 농어의 길이 뿐만 아니라 높이, 두께라는 여러 가지 특성으로 무게를 예측해보자. 이렇게 되면 2차원이 아닌 3차원 공간에서 그래프를 그려야 한다. 이와 같이 특성을 추가하거나 특성을 조합하는 행위를 특성공학이라고 부른다.

판다스 라이브러리를 이용해 데이터셋을 구성한다. 판다스의 핵심 데이터 객체는 DataFrame으로, 마치 엑셀 파일처럼 데이터를 다룰 수 있다는 특징이 있다. (통계, 그래프화 등의 기능을 제공)
csv 파일을 열어보면 각 열마다 농어의 길이(0열), 높이(1열), 너비(2열)가 주어진다. 판다스의 read_csv 메소드를 사용해 csv 파일을 읽어와 dataFrame 객체를 생성하자. 그리고 to_numpy 메소드로 dataFrame 객체를 넘파이로 변환하자.

주어진 농어의 특성들을 조합해 우리는 여러 가지 새로운 특성을 만들 수 있다. preprocessing 모듈의 PolynomialFeature 클래스가 이러한 특성 공학 기능들을 제공한다.
| 객체 생성 -> fit (degree 파라미터의 디폴트 값은 2) -> transform -> 결과: [1, 2, 3, 2^2, 2*3, 3^2] |
이렇게 PolynomialFeatures 클래스는 변환기(Transformer), LinearRegressior, KN-Neighbors.. 와 같이 모델링에 사용되는 클래스는 추정기(Estimator)라고 부른다.
- 변환기의 메소드 순서: fit -> transform ( = 합쳐서 fit_transform() 메소드로 한번에 처리 가능)
- 추정기의 메소드 순서: fit -> predict -> score

poly = PolynomialFeatures(include_bias=False)절편을 위한 특성(1)을 빼기 위해 include_bias = False로 지정한다.
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly.shape)
(42, 9)fit과 transform에 train_input을 넣고 실행하면 42행 9열의 다항 특성 배열을 얻을 수 있다.
poly.get_feature_names()
['x0', 'x1', 'x2', 'x0^2', 'x0 x1', ..., 'x2^2']배열에서 각각의 열이 어떤 값을 의미하는지 궁금하다면 get_feature_names() 메소드를 사용해보자.
(x0은 첫 번째 특성을, x1은 두 번째 특성을 의미한다.)
test_poly = poly.transform(test_input)테스트용 데이터셋의 다항 특성(test_poly)도 구한다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
0.9903183436982124
print(lr.score(test_poly, test_target))
0.9714559911594134LinearRegression에서 fit 메소드로 훈련시킨 다음, 두 훈련 모델의 정확도를 출력해보면 약간의 차이가 존재한다.

정확도를 높이기 위해 degree=5로 설정하고 다항 특성을 만들어보자! 42행 55열의 다항 특성 배열이 생성되었고, 훈련 데이터셋으로 학습한 모델은 거의 완벽한 정확도를 나타낸다. 하지만 테스트 데이터셋은 마이너스 값의 정확도를 띠고 있다.
특성이 55개라서, 데이터(42개) 하나하나를 대응해도 특성이 남기 때문에 .. 과대적합이 발생하는 것이다. 이 과대적합을 막기 위해서는 규제를 적용해야 한다. 규제란 가중치를 보다 줄여서 그래프의 기울기를 완화시키는 방법을 말한다.

규제를 하기 이전에 특성들의 기울기가 비슷해야 하기 때문에 표준화, 즉 스케일 조정이 필요하다.
preprocessing 모듈 밑의 StandardScaler 클래스를 사용한다. 객체를 만들고, fit 메소드에 다항 특성인 train_poly를 넣어 특성을 분류한다. 그 다음, transform 메소드로 분류한 특성들을 표준화한다.

Ridge 클래스를 사용해 릿지 회귀를 할 수 있다. 릿지 회귀는 가중치를 제곱해서 규제하는 회귀 방법이다. L2 규제라고 부르기도 한다. 릿지 회귀를 적용하면 이전과 다르게 두 모델의 정확도가 매우 비슷한 것을 확인할 수 있다.
Ridge() 클래스에는 매개변수 alpha가 존재하는데 alpha의 기본값은 1로 설정되어 있다. alpha가 커질 수록 규제의 강도가 커지며, 이렇게 우리가 직접 정해줘야 하는 값을 '하이퍼 파라미터'라고 부른다. 반대로 가중치는 모델이 학습하는 값이므로 '모델 파라미터'라고 부른다.
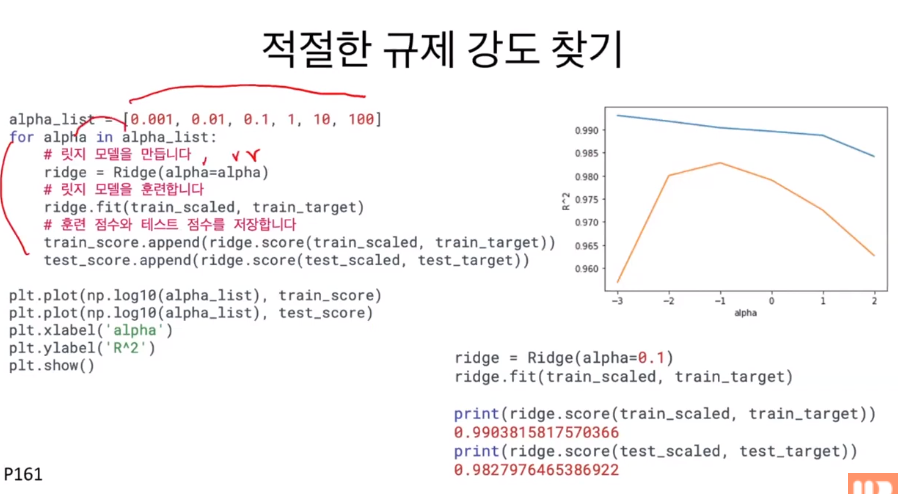
그렇다면 for문을 돌려 리스트에 있는 모든 값들을 alpha 파라미터에 넣어보고 적합한 alpha 값을 찾아보자.
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)x축의 간격을 동일하게 해주기 위해 리스트에 들어있는 값에 각각 log10을 곱한다.
결과 그래프를 보면 alpha가 -1(기존 값 0.1)일 때 가장 높고, 그 뒤로는 alpha 값이 높아질 수록 낮아진다.
이 때, 그래프의 왼쪽은 과대적합(규제 X)인 경우이고, 그래프의 오른쪽은 과소적합(규제가 과함)이 적용된 경우이다.
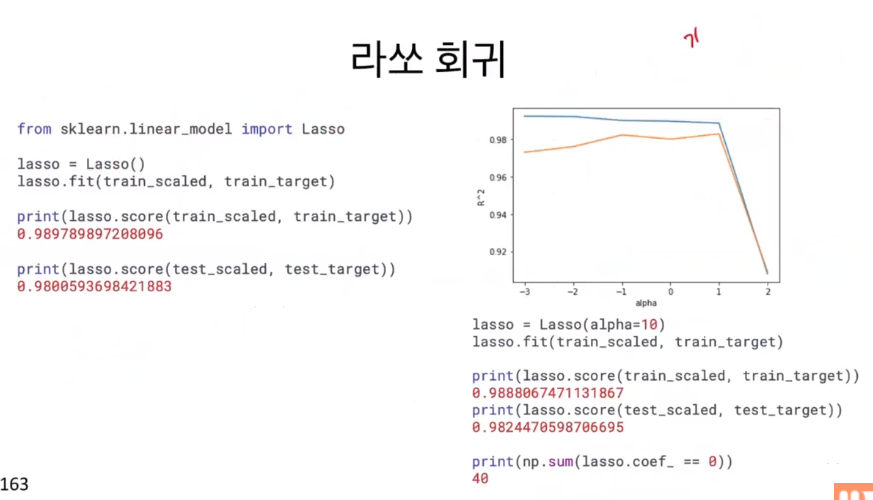
릿지 회귀 외에 또 하나의 규제 방법으로 라쏘 회귀가 있다. 가중치의 절대값을 사용하는 라쏘 회귀는 L1 규제라고 부른다. Lasso 라는 별도의 클래스로 라쏘 회귀를 사용할 수 있다.
라쏘 회귀에서도 alpha 파라미터가 존재한다. 오른쪽 그래프를 보면 alpha가 10일 때 가장 정확도가 비슷하고 높은 것을 확인할 수 있다. 라쏘는 일부 특성을 아예 사용하지 않는다는 특징이 있으며, 사용하지 않는 특성들은 가중치를 0으로 만들어버린다. 위에서는 총 55개 중에서 총 40개의 특성를 사용하지 않는다. 이러한 특징 때문에 일반적으로는 L2 규제가 조금더 효과적이라고 한다.
'ML' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 6장 K-평균 리뷰 (0) | 2022.06.10 |
|---|---|
| 혼자 공부하는 머신러닝 + 딥러닝 6장 군집 알고리즘 리뷰 (0) | 2022.06.10 |
| 혼자 공부하는 머신러닝 + 딥러닝 5장 리뷰 (0) | 2022.05.04 |
| 혼자 공부하는 머신러닝+딥러닝 4장 리뷰 (0) | 2022.04.27 |
| 혼자 공부하는 머신러닝 + 딥러닝 1장 리뷰 (0) | 2022.04.06 |
- Total
- Today
- Yesterday
- 백준27219
- linuxawk
- 버추억박스오류
- 사용자ID
- atq
- SELECT #SELECTFROM #WHERE #ORDERBY #GROUPBY #HAVING #EXISTS #NOTEXISTS #UNION #MINUS #INTERSECTION #SQL #SQLPLUS
- 백준27211
- cron시스템
- GitHubAPIforJava
- whatis
- 쇼미더코드
- linuxtouch
- baekjoon
- Baekjoon27219
- Linux
- OnActivityForResult
- api문서
- awk프로그램
- 리눅스
- 백준
- 버추억박스에러
- Baekjoon27211
- linux파일
- GithubAPI
- E_FAIL
- linuxgedit
- 리눅스cron
- virtualbox
- cat
- 코테
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
