티스토리 뷰
[무료] 혼자 공부하는 머신러닝+딥러닝 - 인프런 | 강의
한빛미디어 혼공시리즈로 1:1 과외하듯이 배우는 초절정 머신러닝, 딥러닝 자습서, 수백 개의 손그림으로 이해하고 구글 코랩(Colab)을 통해 브라우저만 있으면 바로 실습 가능, - 강의 소개 | 인프
www.inflearn.com
로지스틱 회귀

럭키백 속의 물고기가 도미일 확률을 예측해보고자 한다.

길이, 높이, 두께, 대각선 길이, 무게까지 총 5개의 특성을 이용할 것이다.
위의 그림처럼 x의 이웃 샘플 10개 중에서 해당 객체가 몇 개 존재하는가에 따라 확률을 따질 수 있다.

가장 먼저 판다스 라이브러리로 csv 파일을 읽어오자. 판다스의 head 메소드는 읽어온 csv 파일을 테이블로 출력한다.
6개의 열 중에서 Species가 타깃 데이터가 되고, 나머지 5개의 열이 특성 데이터가 된다.

k=3으로 잡고 k-최근접 이웃 다중 분류(KNeighborsClassifier)를 실행한다.
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
classes_ 를 호출하면 타겟 클래스들을 확인할 수 있다. (총 7개의 타겟 클래스가 있음)
print(kn.classes_)
['Bream', 'Parkki', 'Perch', 'Pike', 'Roach', 'Smelt', 'Whitefish']
테스트 데이터셋에서 5개의 데이터를 뽑아 예측하면 다음과 같은 결과가 나타난다.
print(kn.predict(test_scaled[:5]))
['Perch', 'Smelt', 'Pike', 'Perch', 'Perch']
확률을 확인하고 싶을 땐 predict_proba를 사용한다. 5개의 샘플에 대해 7개의 생선(클래스)에 대한 확률이 출력된다.
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=4))
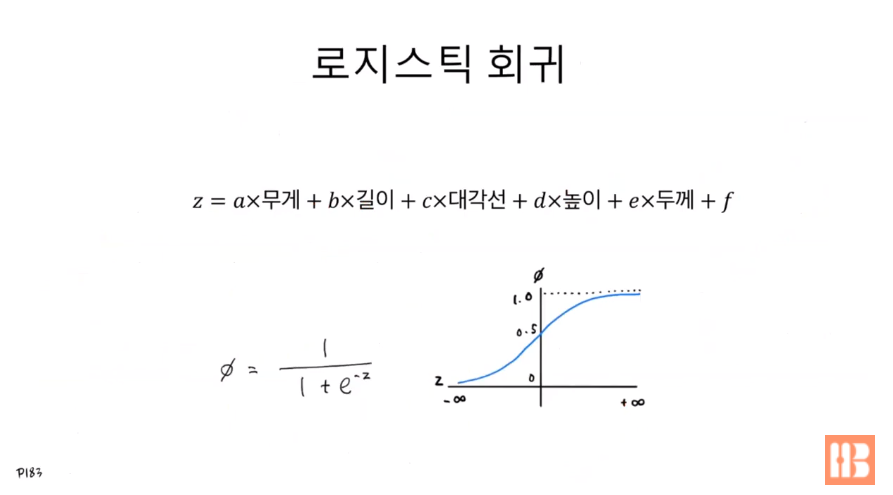
대표적인 분류 알고리즘으로 로지스틱 회귀가 있다. (이름에만 회귀가 들어갈 뿐 회귀 알고리즘이 아니다.)
계수(a, b, c, d, e)가 특성의 개수만큼 필요하며, 결과값 z를 그대로 사용하면 회귀가 되기 때문에 0~1 범위의 값으로 압축해 확률을 표현하도록 한다. z 값 압축에 사용되는 함수를 시그모이드 함수(=로지스틱 함수)라고 하며 위의 그래프와 식이 여기에 해당한다. 확률 값이 0.5보다 크면 양성 클래스, 작으면 음성 클래스라고 볼 수 있다.

가장 먼저 다중 분류보다 간단한 이진 분류를 다뤄보자. 불리언 인덱싱을 사용해 도미와 빙어 데이터만 불러와 훈련 데이터와 타겟 데이터를 만들자. 그 다음, LogisticRegression 클래스를 사용해 로지스틱 회귀를 적용한다.
predict_proba로 확률을 출력하면 0번째 열이 음성 클래스일 확률을, 1번째 열이 양성 클래스일 확률을 나타낸다.

coef_와 intercept_에는 각 특성의 계수가 담겨 있고, decision_function 메소드를 사용하면 해당 데이터의 z 값을 리턴한다. 시그노이드 함수에 넣어 확률값이 정확하게 나오는지 확인해보자. scipy의 expit을 호출하면 시그노이드 함수에 z 값을 적용했을 때의 확률 값을 볼 수 있다. (양성 클래스의 확률값)

이번에는 다중 분류를 적용해보자. max_iter 파라미터는 반복 횟수를 의미한다.
로지스틱 회귀에는 L2 규제가 기본적으로 적용되어 있다. 파라미터 C의 값이 클수록 규제가 약해지고, 작을 수록 규제가 강해진다. C의 기본값은 1인데, 20으로 높여 규제를 약하게 적용해주었다.
predict_proba 메소드를 사용하면 5개의 행에 대해 7개의 확률(클래스)이 출력된다. 계수의 크기를 출력해보면 역시 7개의 행(클래스)과 5개의 열(계수)이 있다는 것을 알 수 있다.

다중 분류에서는 시그노이드 함수 대신에 소프트맥스 함수로 z 값을 0~1 사이의 값으로 압축한다.
확률적 경사 하강법
럭키 백이 대박 나서 많은 수의 어민들이 자기들이 잡은 생선을 럭키 백에 넣어달라고 한다. 생선이 추가될 때마다 가중치는 유지하되, 모델은 업데이트하고 싶다면 어떻게 해야할까? => 점진적 학습, 온라인 학습!
점진적 학습 방법 중 하나로 확률적 경사 하강법이 있다. 확률적 경사 하강법은 머신러닝 알고리즘은 아니지만 딥러닝 알고리즘을 보다 최적화할 수 있는 알고리즘이다.
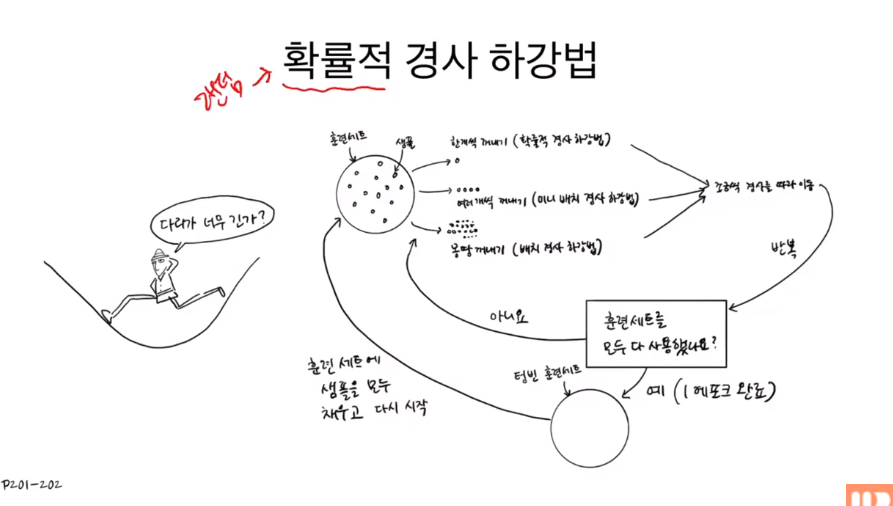
확률적 경사 하강법에서는 최저점을 건너 뛸 수도 있기 때문에 아주 조금씩..? 경사를 내려가야 한다고 말한다. 훈련 데이터셋에서 샘플을 하나씩 꺼내 조금씩 경사를 이동하도록 한다. 이 과정을 반복해 훈련 데이터셋을 모두 사용하면 1 에포크(epoch)를 완료한 것이다. 이제 다시 훈련 데이터셋에 샘플을 채우고 다시 처음부터 훈련을 시작한다.
한번에 여러 개의 샘플을 꺼내 사용하면 미니 배치 경사 하강법, 샘플을 몽땅 꺼내서 사용하면 배치 경사 하강법이라고 한다.
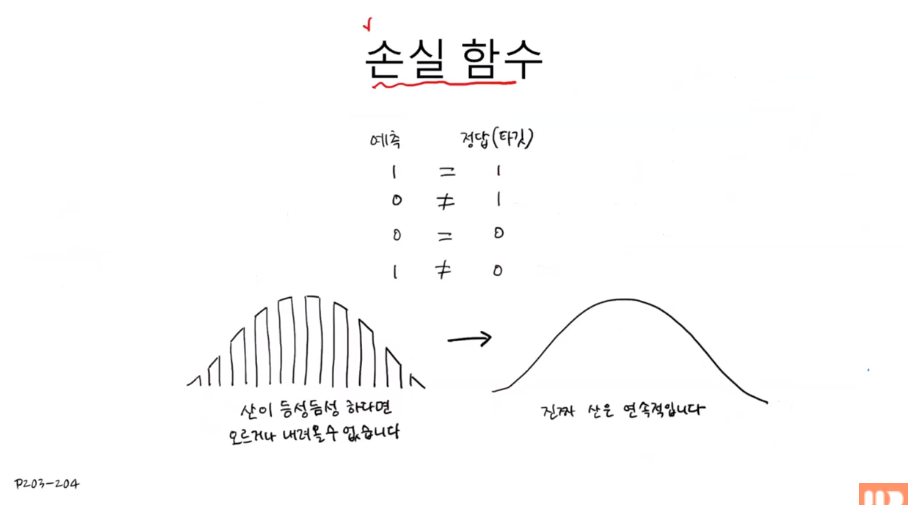
손실 함수는 머신러닝 알고리즘이 얼마나 나쁜지 그 정도를 측정하는 함수이다. 손실 함수의 값이 낮아지는 방향으로 가중치와 계수를 변경하도록 한다. 이전 시간에 배운 분류 알고리즘은 정확도를 사용했었는데... 정확도는 0, 0.25, 0.5, 0.75, 1과 같이 듬성듬성하게, 비연속적인 값을 갖고 있기 때문에 손실 함수로 사용할 수 없다고 한다. (미분이 불가능하므로)

회귀는 평균 절대값 오차 또는 평균 제곱 오차 함수를 사용하는데, 이 두 가지 값은 연속적인 값, 즉 미분 가능한 값이기 때문에 손실 함수를 사용할 수 있다. 그러나 분류는 정확도로 성능을 따지기 때문에 손실 함수를 사용할 수 없고, 대신에 로지스틱 손실 함수로 알고리즘을 최적화한다.
정답이 1인 데이터를 0.9로 예측한 경우에는 마이너스만 붙여 -0.9라는 손실 값을 갖도록 한다. 그러나 만약 정답이 0인 데이터를 0.2로 예측했다면 두 값을 반대로 바꿔 정답이 1인 데이터를 0.8로 예측했다고 가정해 -0.8이라는 손실 값을 갖도록 한다. 이 방식으로 [-0.9, -0.3, -0.8, -0.2]의 손실 값이 나타난다.
이 과정을 식으로 나타내면
(1) target = 1일 때, -log(예측 확률)
(2) target = 0일 때, -log(1 - 예측 확률)
으로 표현할 수 있다.

각각의 특성마다 스케일이 다르면 경사를 제대로 판단할 수 없기 때문에 전처리가 필요하다.
StandardScaler 클래스를 사용해 데이터의 스케일을 조정하자.

확률적 경사 분류 알고리즘은 SGDClassifier 클래스가, 확률적 경사 회귀 알고리즘은 SGDRegressor 클래스가 제공하고 있다. loss 파라미터에는 사용하고 싶은 로지스틱 함수를 지정하고, max_iter 파라미터에는 epoch 값을 지정한다.
partial_fit 메소드를 사용하면 기존의 가중치를 유지하면서 다시 학습시킬 수 있다.
아쉽게도 SGDClassifier는 배치와 미니 배치 경사를 지원하지 않는다고한다.
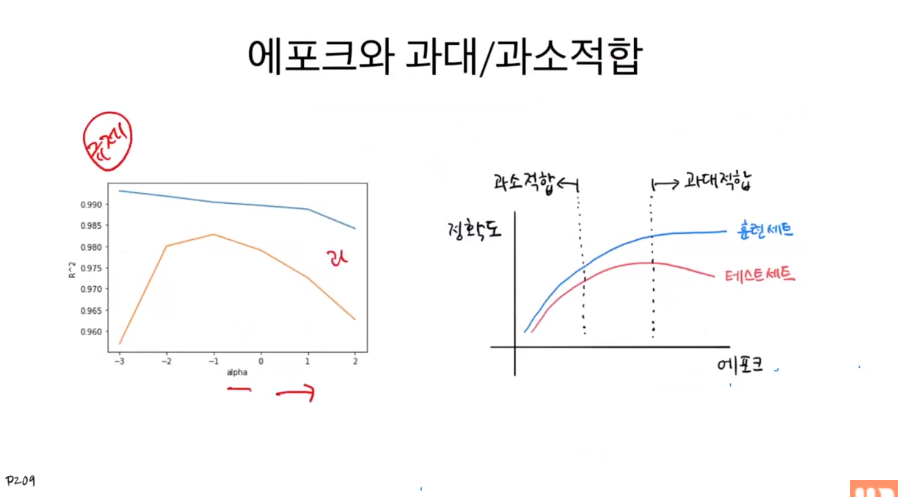
규제와 마찬가지로 에포크도 두 정확도의 차이가 가장 적으면서 정확도가 높은 적절한 값을 찾아야 한다.
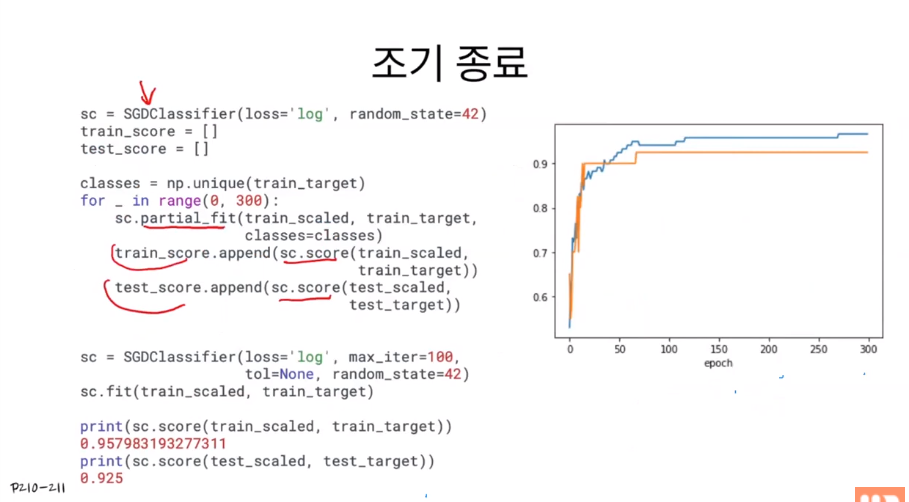
partial_fit은 데이터셋의 일부분만 학습시키는 것이다 보니 전체 클래스의 일부분만이 데이터셋에 존재할 수도 있다. 그래서 전체 클래스 리스트를 classes 파라미터로 전달해주어야 한다.
class = np.unique(train_target)
for _ in range(0, 300) :
sc.partial_fit(train_scaled, train_target, classes=classes)
오른쪽의 그래프를 통해 epoch가 100일 때가 가장 적절하다는 것을 확인할 수 있다. max_iter에 100을 지정하고 확률적 경사 분류를 실행하면 정확도가 비슷해진 것을 확인할 수 있다.
sc = SGDClassifier(loss='log', max_iter=100, tol=None, random_state=42)
'ML' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 6장 K-평균 리뷰 (0) | 2022.06.10 |
|---|---|
| 혼자 공부하는 머신러닝 + 딥러닝 6장 군집 알고리즘 리뷰 (0) | 2022.06.10 |
| 혼자 공부하는 머신러닝 + 딥러닝 5장 리뷰 (0) | 2022.05.04 |
| 혼자 공부하는 머신러닝+딥러닝 3장 리뷰 (0) | 2022.04.27 |
| 혼자 공부하는 머신러닝 + 딥러닝 1장 리뷰 (0) | 2022.04.06 |
- Total
- Today
- Yesterday
- OnActivityForResult
- 백준27219
- atq
- linuxtouch
- awk프로그램
- 리눅스cron
- 백준
- 백준27211
- 사용자ID
- virtualbox
- api문서
- GitHubAPIforJava
- linux파일
- 버추억박스에러
- SELECT #SELECTFROM #WHERE #ORDERBY #GROUPBY #HAVING #EXISTS #NOTEXISTS #UNION #MINUS #INTERSECTION #SQL #SQLPLUS
- whatis
- linuxawk
- Linux
- cron시스템
- 버추억박스오류
- linuxgedit
- 리눅스
- GithubAPI
- 코테
- Baekjoon27219
- E_FAIL
- 쇼미더코드
- Baekjoon27211
- cat
- baekjoon
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
